Deep neural networks (DNNs) have achieved state-of-the-art performance across many domains, largely due to their over-parameterized nature. However, this comes at a cost—high memory usage, slow inference, and limited deployability on edge devices. In this work, we explore a new method to uncover Strong Lottery Tickets (SLTs) using a fully differentiable, training-free approach based on Continuously Relaxed Bernoulli Gates (CRBG).
Motivation
The Lottery Ticket Hypothesis (LTH) suggests that a small subnetwork within a large DNN, when trained in isolation, can match the performance of the original. A Strong Lottery Ticket (SLT) takes this further—achieving such performance without any weight updates.
Existing SLT methods like edge-popup require surrogate gradients or non-differentiable ranking, which limits scalability. Our method introduces a differentiable gating mechanism that learns sparse masks directly at initialization, keeping weights frozen.
Method Overview
The proposed method applies CRBGs to prune networks in both unstructured and structured fashions.
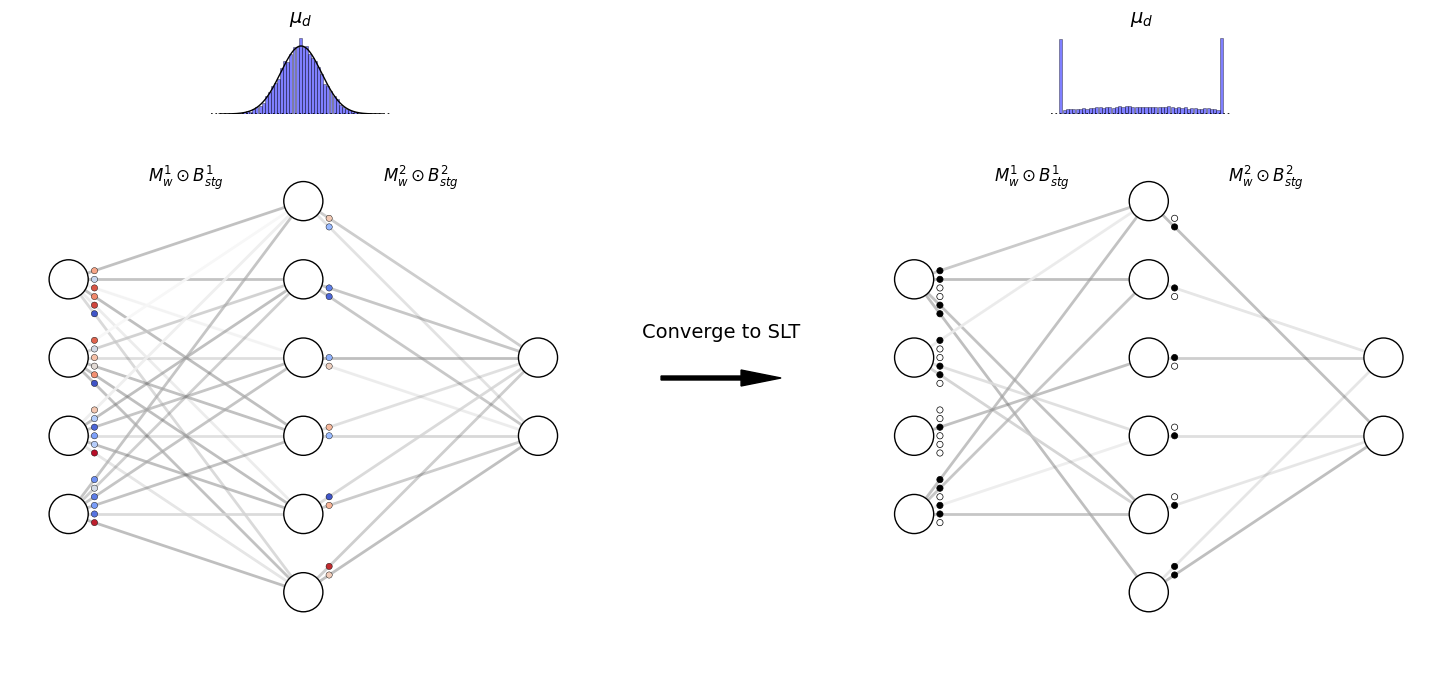
Unstructured Pruning
Each weight is gated using:
\[z_{ij}^l = \max(0, \min(1, \mu_{ij}^l + \epsilon_{ij}^l)), \quad \epsilon_{ij}^l \sim N(0, \sigma^2)\]The output of layer $i$ becomes:
\[\widetilde{G}^{(i)}(x) = \sigma(B^{(i)} \odot W^{(i)} x)\]where $B^{(i)}$ is the binary mask and $\odot$ denotes element-wise multiplication.
A sparsity-inducing regularization is applied:
\[R = \lambda \sum_{i,j,l} \Phi\left(\frac{\mu_{ij}^l}{\sigma}\right)\]Structured Pruning
CRBGs are applied at the neuron level:
\[z_d^l = \max(0, \min(1, \mu_d^l + \epsilon_d^l))\]Each layer output becomes:
\[h^{(i)} = g^{(i)} \odot \sigma(W^{(i)} h^{(i-1)})\]The objective combines prediction loss and a sparsity penalty:
\[\min_{W^{(i)}, g^{(i)}} L(\{g^{(i)} \odot \sigma(W^{(i)} h^{(i-1)})\}) + \lambda \sum_{i=1}^{L} \|g^{(i)}\|_0\]Initialization Strategy
We use a uniform distribution:
\[W \sim U[-\alpha, \alpha]\]This avoids scaling heuristics like Xavier or Kaiming since weights remain fixed during the gating optimization.
Experiments
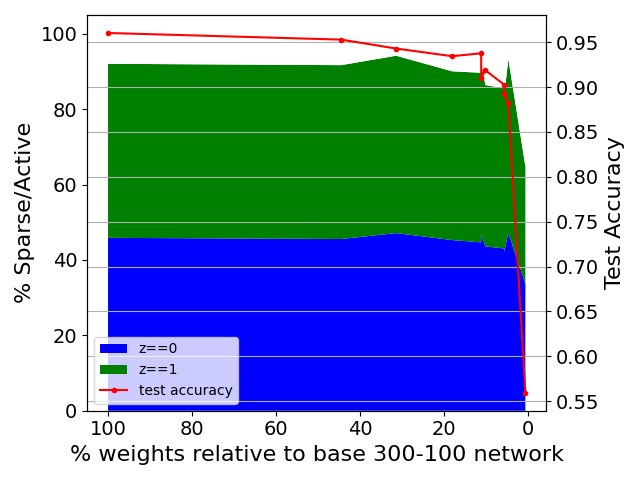
LeNet-300-100 on MNIST
- Achieved 88% test accuracy with 77% structured sparsity
- PreReLU used instead of ReLU to avoid unintentional sparsification
- Compared regularization strategies: induce-decision outperformed induce-sparse
CNNs on CIFAR-10
- ResNet-50: 83.1% accuracy, 91.5% weight sparsity
- Wide-ResNet50: 88% accuracy, 90.5% sparsity
- Observed higher sparsity in deeper layers, confirming redundancy in late-stage representations
Transformers
ViT-base
- 76% accuracy, 90% sparsity
- First strong lottery ticket discovered in vision transformers
Swin-T
- 80% accuracy, 50% sparsity
These results show our method scales to modern architectures and outperforms prior SLT discovery methods.
Comparison Table (Excerpt)
| Method | Architecture | Accuracy | Sparsity | Trained Weights |
|---|---|---|---|---|
| Ours (CRBG) | LeNet-300-100 | 96% | 45% | ❌ |
| edge-popup (SLTH) | 500-500-500-500 | 85% | 50% | ❌ |
| Sparse VD | 512-114-72 | 98.2% | 97.8% | ✅ |
Key Contributions
- Differentiable pruning using relaxed Bernoulli variables
- Supports both structured and unstructured sparsity
- Weight-free subnetwork discovery at initialization
- Applies to CNNs, FCNs, and Transformers
- Outperforms state-of-the-art in accuracy and sparsity trade-off
Future Work
Promising directions include:
- Adaptive regularization and variance learning
- Multi-level and hierarchical gating schemes
- Application to NLP, GNNs, and RNNs
- Theoretical analysis of convergence and expressivity
- Hardware-aware deployment for edge devices
Conclusion
This thesis proposes a scalable, training-free method to uncover Strong Lottery Tickets using Continuously Relaxed Bernoulli Gates. By enabling high sparsity and strong performance across diverse architectures, we take a step toward efficient, deployable, and interpretable deep learning.